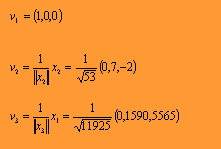A un conjunto de vectores , donde n, es   el número de    vectores   en el conjunto, se le conoce como base si lo vectores son Linealmente    Independientes (LI).    Existen también   bases de   que pueden ser ortonormales, es decir,   que vectores a   pares de la base son ortogonales entre   sí    y además todos los vectores de la base son unitarios.    Esta propiedad tiene    algunas    aplicaciones interesantes matemáticamente. Por ejemplo, se utiliza la ortonormalización en la mecánica   cuántica para describir a un sistema.

El proceso para convertir una base cualquiera en una base ortonormal sigue los siguientes pasos:

1. Se aplica el proceso de ortogonalización de Gram-Schmidt.
2. Se normalizan todos los vectores de la base.

Obviamente la   parte más complicada es    la ortogonalización. El método    de   Gram-Schmidt se fundamenta en convertir dos vectores cualesquiera en ortogonales, a partir de la adición  vectorial a uno de los vectores.

El objetivo de este proceso es convertir una base Y no ortogonal en otra base X ortogonal a partir de los vectores de Y. Por ejemplo, se tiene la base                                     y   a   partir  de   ella se quiere formar una nueva base                                     que es ortogonal.

El primer vector de la nueva base X será naturalmente       es decir,             Después   habrá   que agregar a la base de X un nuevo vector       que  sea ortogonal a      pero este nuevo  vector  debe construirse a partir de        , es decir, nuevamente ocupamos la base Y para obtener a la base X. Se puede suponer el siguiente razonamiento:

  

  

 

 

 

 

 

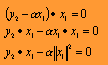
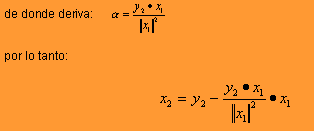
Así, se puede  deducir que para casos más generales, en donde los vectores son   de   dimensiones superiores a 2, hasta n. Se aplica la misma fórmula. Para el enésimo caso de la nueva base se tiene:

 

 

 

 

 

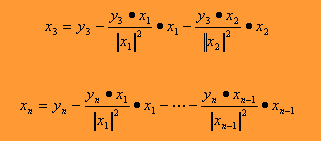
Ese es pues el proceso de ortogonalización de Gram-Schmidt. Claro, es latoso pero eficiente.

La normalización no debe  resultar problemática, se trata simplemente  de obtener   la magnitud   de cada uno de los vectores ya ortogonalizados (base X) y dividir cada uno de estos vectores entre su vector correspondiente. Es decir:

 

 

 

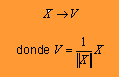
Ejemplo:

Dada la siguiente base                                                       obtener una base ortonormal V.

Sabemos que:                                                                 Así, siguiendo el método:

 

 

 

 

 

 

 

 

 

 

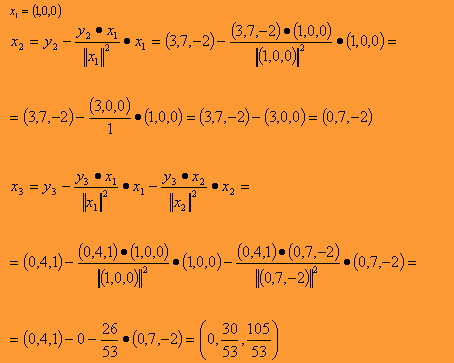
Finalmente normalizando cada uno de estos vectores de la base X obtenemos la base V buscada.